Byton Tree [B]

Memory limit: 128 MB

Bytons grow on a byton tree. They are rare fruits and they can only be found on branches from which no other branches grow.

All bytons growing on a single branch have the same time interval in which they can be picked. If they are picked too early, they will be unripe, and if too late, they will be rotten. Every person owning a byton tree wonders how many cuts need to be performed for all bytons to be collected and for each collected byton to be eatable in the moment it is picked. Cuts can be performed at each branch, near its beginning. When a cut is performed, all bytons growing directly or indirectly on the corresponding branch are picked. We assume that an arbitrary number of cuts can be performed in one unit of time and that the trunk is also a branch.

Input

The first and only line of the standard input contains a description of a byton tree, written in a recursive manner. The first integer denotes the number of branches growing on the trunk; it is followed by the descriptions of these branches. A description of a branch consists of the number of branches that grow on it, followed by descriptions of these branches. If any bytons grow on a branch, 0 is written as the number of branches growing on it and it is followed by two integers 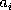, 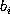(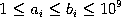) which denote the time interval when the bytons can be collected. The total number of all branches does not exceed .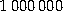

Output

The first and only line of the standard output should contain a single integer denoting the minimal number of cuts that need to be performed for all the picked bytons to be eatable.

Example

For the input data:

2 1 0 3 5 2 0 8 10 1 0 6 9

the correct result is:

2

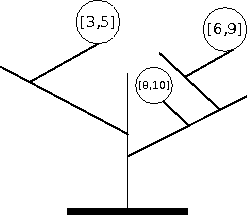
Explanation of the example: The byton tree from the example contains 3 branches on which bytons grow - the intervals in the figure represent their periods of eatability. In order to collect all bytons, 2 cuts are sufficient: the first one can be performed e.g. in moment 5, the second one in moment 8.

Task author: Jacek Tomasiewicz.